Solving SAT problems using the model method
From national Singapore Math trainer, Cassy Turner at http://www.singaporemaths.com/:
David Marin over at MathNotations has been periodically tweeting an SAT problem of the day via @dmarain. A recent series of tweets asked:
First model the beginning mixture at 6:1.
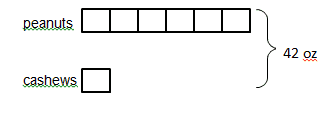
Next, we can figure out how many units need to be added to the cashews to make the cashews to peanuts ratio 2:1.
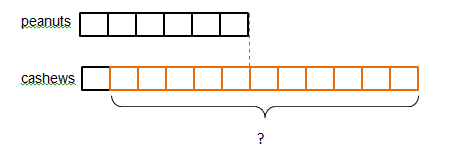
Since there are 11 additional units and the value of each unit is 6 oz, we can find the value of the added cashews.
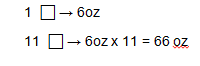
66 ounces of cashews must be added to the peanuts to make the mixture 2:1.
"Content from http://SingaporeMathSource.com (c) Cassandra Turner reproduced courtesy of the Author."
A 42 oz mix of nuts is 6 parts peanuts to 1 part cashews. How many ounces of cashews must be added to make a make the mixture 2 parts cashews to 1 part peanuts? Does Singapore (bar) model method work here?Sure it can! Here’s one solution.
First model the beginning mixture at 6:1.

Next, we can figure out how many units need to be added to the cashews to make the cashews to peanuts ratio 2:1.

Since there are 11 additional units and the value of each unit is 6 oz, we can find the value of the added cashews.
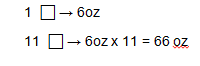
66 ounces of cashews must be added to the peanuts to make the mixture 2:1.
"Content from http://SingaporeMathSource.com (c) Cassandra Turner reproduced courtesy of the Author."